Bestimmen von Minima und Maxima nochmal kurz zusammengefasst:

1) Sucht Kritische Punkte:

-0-Stellen der Ableitung der Funktion
-Stellen, an der die Ableitung der Funktion nicht definiert ist. (Hier könnte eine Sprungstelle sein!)

-Falls ein fixer Definitionsbereich vorgegeben ist : Randstellen des Definitionsbereichs


2)Stellt fest, welche davon wirklich Extrema sind

D.h. für Punkte innerhalb des Definitionsbereichs:
Wechselt die Ableitung der Funktion das Vorzeichen? 

Wechselt die Ableitung an diesem Punkt das Vorzeichen von + auf - , ist der Punkt ein Maximum.
Wechselt die Ableitung an diesem Punkt das Vorzeichen von - auf + , ist der Punkt ein Minimum.

Willst du einen kritischen Punkt x = a untersuchen, der eine 0-Stelle der Ableitung ist, gilt folgendes:

-Ist die doppelte Ableitung an diesem Punkt f ‘‘(a) kleiner 0, liegt dort ein Maximum.
-Ist die doppelte Ableitung an diesem Punkt f ‘‘(a) größer 0, liegt dort ein Minimum.
-In allen anderen Fällen musst du den Punkt anders überprüfen!

Kannst du begründen, warum der obige Trick funktioniert? Schreibe deine Begründung in dein 
Hausübungs-Heft! Versuche vielleicht eine Skizze zu zeichnen! 

Wozu brauchen wir jetzt unser erworbenes Wissen?
Nun, wir können jetzt Extremstellen von Funktionen finden. Das kann sehr nützlich sein, da viele
Vorgänge in der Natur und im Alltagsleben durch Formeln bzw. Funktionen beschrieben werden
können! 

Ein Beispiel:

Ein Bauer will mit 60 Laufmetern Maschendraht einen rechtwinkligen Hühnerhof an eine Mauer 
bauen. Welche Abmessungen soll er wählen, damit der Flächeninhalt möglichst groß wird?



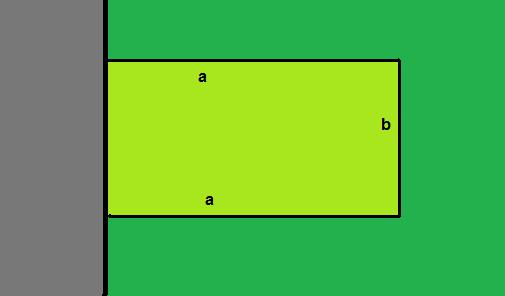Wir bezeichnen die Länge des Hühnerhofs mit a, die Breite mit b. Wir haben 60m Draht. Aus der
Skizze sehen wir:

60 = 2a + b

Oder anders:

b = 60 – 2a

Die Fläche des Hühnerhofs beträgt:

A = a * b


Wir setzen nun ein:

A = a * b = a *  (60 – 2a) = 60a – 2a²


Wir haben also eine Formel für die Fläche die nur mehr von a abhängt!

Nun leiten wir ab (und zwar nach a):

d A (a) / da = A‘(a) = 60 – 4a


Die Ableitung dieser Funktion ist überall definiert und hat keine Sprungstellen, aber wir können
nach 0-Stellen suchen!

0 = 60 – 4a

Wir schreiben um:

4a= 60

bzw.

a = 60/4 = 15


Wir können prüfen, ob es sich hier wirklich um ein Maximum handelt:
A‘‘(a) = -4
A‘‘(15) = -4 < 0

Damit haben wir gezeigt, dass A(15) ein Maximum ist. Da wir keine anderen kritischen Punkte haben,
ist es sogar das globale Maximum. Damit haben wir unsere Lösung:

a = 15
b = 60 – 2a = 30

Versuche die folgenden Übungsaufgaben zu lösen. Es ist immer ein Link mit einer Lösung angeben.
Vergleiche deine Ergebnisse mit den Lösungen! Diskutiert eure Ergebnisse und Rechenwege
in der Klasse!

Aufgabe 1:
Bestimme die Seitenlänge, die nötig ist, damit ein Rechteck mit 40cm Umfang den maximalen 
Flächeninhalt erreicht!

Lösung Aufgabe 1


Aufgabe 2:
Bestimme die Extrema von f(x) = x² + 2x +1
Welche davon sind globale Extrema?

Lösung Aufgabe 2


Aufgabe 3:
Bestimme die Extrema von f(x) = x² + 2x +1 im Bereich [-2,1]
Welche davon sind globale Extrema?

Lösung Aufgabe 3


Aufgabe 4:
Bestimme die Extrema von f(x) = x5 + 3x² + 2
Welche davon sind globale Extrema?

Lösung Aufgabe 4