Wie bereits im ersten Kapitel erwähnt, beschreibt die Ableitung einer Funktion ihre Steigung.
Was bedeutet das aber?

Betrachten wir ein Beispiel:
Wir haben eine gerade Straße. Vor dieser Straße steht folgendes Schild:



Dieses Schild sagt uns, dass diese Straße eine Steigung von 10%, bzw. in ganzen Zahlen von  0,1 hat.
D.h. nach einem Meter verläuft sie um 0,1 Meter höher, nach 10 Metern um 1 Meter, nach 20
Metern um 2 Metern, usw.
Die Straße (also die Höhe des Straßenverlaufs) verhält sich wie eine lineare Funktion:

y=kx+d        mit k=0,1

Wie ihr nennt man k die Steigung der linearen Funktion.

Wenn wir nun statt k = 0,1 einen höheren Wert einsetzen, wächst y (also der Straßenverlauf) 
schneller.

Dies kannst du in der folgenden Graphik sehen:
y= 0,1*x (blau)
y= 1*x (rot)



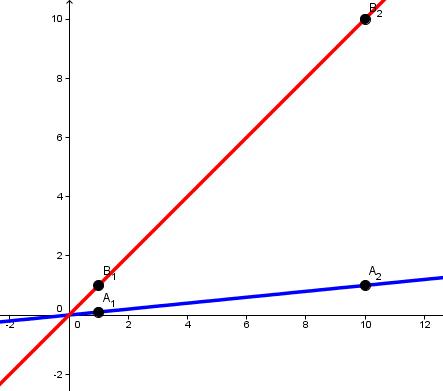Je höher der Wert für k ist, also je größer die Steigung, desto stärker wächst die Funktion.
Setzt du einen negativen Wert ein, fällt die Funktion mit wachsendem x, und zwar umso stärker,
je größer der Betrag von k ist, d.h. je kleiner k ist.


Im nächsten Fenster kannst du das Ganze selbst ausprobieren.  Die Funktion y = kx wird dargestellt.
Mit dem Schieberegler kannst du den Wert für k einstellen. Versuche was passiert, wenn du ihn veränderst!

Steigung

Leitest du nun y = kx + d ab, erhältst du:

y ‘ = k + 0 = k

Die Ableitung von y = kx + d entspricht also ihrer Steigung. Je größer ihr Wert ist, desto 
steiler verläuft die lineare Funktion. Ist Sie größer als 0, wächst sie mit wachsenden x-
Werten, ist sie kleiner als 0, sinkt sie ab.

Bei anderen Funktionen ist es genauso:

- Ist der Betrag der Ableitung einer Funktion an einer in einem Intervall (bzw. an einer Stelle x) groß,
ist sie dort steil.

-Ist die Ableitung (also die Steigung) in diesem Intervall [a,b] positiv, wächst der Funktionswert mit
wachsenden x-Werten (man sagt, sie ist dort “streng monoton steigend“)

-Ist die Ableitung (also die Steigung) in diesem Intervall [a,b] negativ, sinkt  der Funktionswert mit
wachsenden x-Werten (man sagt, sie ist dort “streng monoton fallend“)

-Ist die Ableitung (also die Steigung) in diesem Intervall [a,b] gleich 0, ändert sich der Funktionswert
mit wachsenden x-Werten überhaupt nicht.  Ihr Graph ist dort eine Gerade parallel zur y-Achse.
(Man sagt, sie ist dort “konstant“)

Ist die Ableitung größer-gleich 0 bzw. kleiner-gleich 0, sagt man sie ist in diesem Bereich 
“monoton wachsend“ oder “monoton fallend“.
Eine monoton steigende Funktion wächst mit wachsenden x-Werten, kann aber zwischendurch auch konstant sein! 

Schauen wir uns das Ganze anhand eines Beispiels an:

f(x) = x²



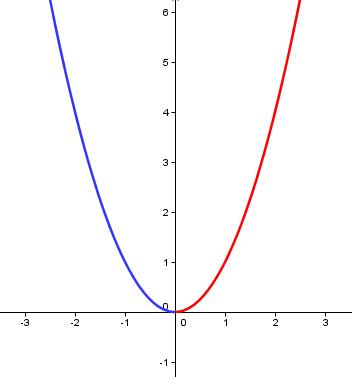f ‘(x) = 2x

Im Bereich x<0 (blau) ist f ‘(x) kleiner 0, die Funktion fällt.
Im Bereich x>0 (rot) ist f ‘(x) größer 0, die Funktion steigt.

Bei x=1 ist der Wert für die Ableitung f ‘(1) = 1 kleiner, als bei x = 2, also f ‘(x) = 4
Darum ist die Funktion bei x = 2 steiler, als bei x = 1.

Für eine Funktion an im Bereich zwischen x1 und x2 gilt:

- Ist der Betrag der Ableitung der Funktion in diesem Intervall
(oder an einer Stelle x) groß, ist sie dort steil.

-Ist f ‘(x) > 0, ist die Funktion dort “streng monoton steigend“
-Ist f ‘(x) &ge 0, ist die Funktion dort “ monoton steigend“

- Ist f ‘(x) < 0, ist die Funktion dort “streng monoton fallend“
- Ist f ‘(x) &le 0, ist die Funktion dort “monoton fallend“

- Ist f ‘(x) = 0, ist die Funktion dort “konstant“

Nun gut, Reisender. Du hast einiges gelernt. Erfülle meine Aufgaben um zu sehen, ob du alles
verstanden hast!

-Schreibe die obige Definition in dein Schulübungs-Heft und überlege nochmal, was die einzelnen 
Punkte aussagen.

-Zeichne die Funktionsgraphen von f(x) = x², g(x) = x³, f ‘(x) und g‘ (x) in dein Hausübungs-Heft.
Schreibe dazu, wo diese Funktionen streng monoton steigend/fallend und wo sie monoton
steigend und fallend sind!

Du scheinst gut voran zu kommen, wenn du hier angelangt bist. Die folgenden Aufgaben sollen dich 
zum Nachdenken anregen. Versuche auf eine Lösung zu kommen!

-Mache dasselbe wie oben für h(x) = sin(x). Was fällt dir auf? Wo hat die Funktion ihre höchsten und 
tiefsten Punkte? (Vergleiche mit der Ableitung)

-Überlege dir:
Ist eine streng monoton steigende Funktion immer monoton steigend, oder findest du ein
Gegenbeispiel? Ist umgekehrt eine monoton steigende Funktion automatisch streng monoton 
steigend?  

-Kann eine Funktion gleichzeitig monoton steigend und monoton fallend sein? Wenn ja, gib ein 
Beispiel, wenn nicht begründe warum!

Begründe deine Aussagen! Gib die Antworten schriftlich ab oder diskutiert sie mit eurem Professor in
der Klasse!