|
4.1 Extrema
|

 

|
Wir haben nun gesehen, was Monotonie bedeutet. Doch wir können mittels der Ableitung einer
Funktion noch mehr über sie aussagen.
Wir wollen uns nun auf die Suche nach sogenannten Extrema machen.
Ein Extremum kann entweder ein Minimum einer Funktion oder ein Maximum einer Funktion sein.
Was genau ist das? Und wo können solche Extrema liegen?
Einleitung
|
|
4.2 Maxima
|

 

|
Ein sogenanntes Maximum einer Funktion ist ein Punkt x = a, dessen Funktionswert f(a) zumindest
für einen kleinen Bereich um diesen Punkt (also links und rechts auf der x-Achse) der größte
Funktionswert ist.
Oder Mathematisch:
Beim Punkt x = a liegt ein Maximum f(a), wenn gilt:
f(a) &ge f(x) in einer näheren Umgebung von a.
Was heißt das jetzt anschaulich?
Schauen wir uns die Funktion f(x) = -x² +2 an:
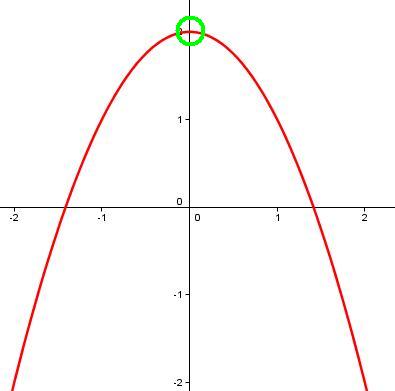 Die Funktion hat bei x = 0 offensichtlich ein Maximum, da sie dort den größten Funktionswert für
eine gewisse Umgebung um 0 hat (z.B. alle Zahlen zwischen -1 und 1 oder -0,5 und 0,5 usw.)
Wir sehen an diesem Beispiel auch folgendes:
Damit ein Punkt x = a ein Maximum sein kann muss die Funktion zumindest in einem kleinen
Bereich x < a wachsen und in einem kleinen Bereich x > a fallen. Sonst kann er ja anschaulich kein
Maximum sein.
Betrachten wir unser Beispiel:
Die Funktion hat bei x = 0 offensichtlich ein Maximum, da sie dort den größten Funktionswert für
eine gewisse Umgebung um 0 hat (z.B. alle Zahlen zwischen -1 und 1 oder -0,5 und 0,5 usw.)
Wir sehen an diesem Beispiel auch folgendes:
Damit ein Punkt x = a ein Maximum sein kann muss die Funktion zumindest in einem kleinen
Bereich x < a wachsen und in einem kleinen Bereich x > a fallen. Sonst kann er ja anschaulich kein
Maximum sein.
Betrachten wir unser Beispiel:
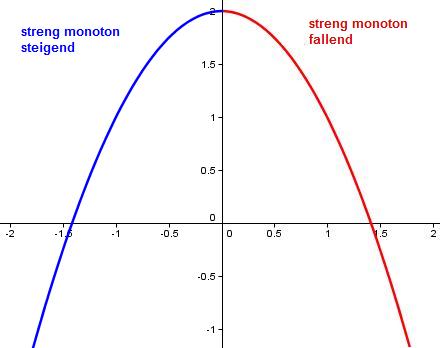
 Die Funktion ist für x < 0 streng monoton steigend, für x > 0 streng monoton fallend. Das heißt alle
Werte in der Nähe von 0 sind kleiner f(0) = 2 und damit ist 2 ein Maximum von f(x) beim Punkt x = 2
Die Funktion ist für x < 0 streng monoton steigend, für x > 0 streng monoton fallend. Das heißt alle
Werte in der Nähe von 0 sind kleiner f(0) = 2 und damit ist 2 ein Maximum von f(x) beim Punkt x = 2
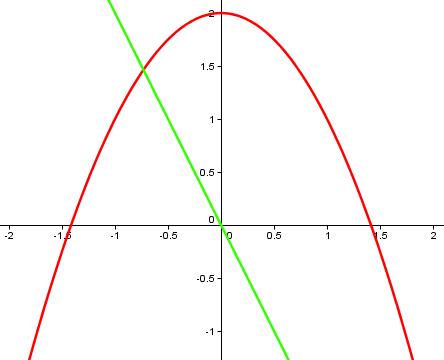
 Schauen wir uns nun die Ableitung von f(x) an:
f ‘(x) = -2x
Schauen wir uns nun die Ableitung von f(x) an:
f ‘(x) = -2x
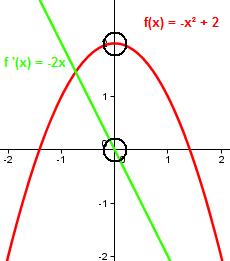
 Wir sehen, es gilt:
f(x) > 0 für x < 0
f(x) < 0 für x > 0
Das ist auch klar, da f(x) ja sonst in den jeweiligen Bereichen nicht streng monoton wachsend bzw.
fallend sein kann. f ‘(x) wechselt also bei x = 0. Das Vorzeichen von + zu - !
Ganz allgemein kann man sagen:
Wechselt die Ableitung f ‘(x) am Punkt x = a ihr Vorzeichen von + auf - , hat f(x) bei x = a
ein Maximum f(a)
Das kann nur bei einer 0-Stelle der Ableitung oder bei einer Sprungstelle der Ableitung passieren!
Ein Beispiel für eine 0-Stelle ist die Funktion von eben:
Wir sehen, es gilt:
f(x) > 0 für x < 0
f(x) < 0 für x > 0
Das ist auch klar, da f(x) ja sonst in den jeweiligen Bereichen nicht streng monoton wachsend bzw.
fallend sein kann. f ‘(x) wechselt also bei x = 0. Das Vorzeichen von + zu - !
Ganz allgemein kann man sagen:
Wechselt die Ableitung f ‘(x) am Punkt x = a ihr Vorzeichen von + auf - , hat f(x) bei x = a
ein Maximum f(a)
Das kann nur bei einer 0-Stelle der Ableitung oder bei einer Sprungstelle der Ableitung passieren!
Ein Beispiel für eine 0-Stelle ist die Funktion von eben:
 Ein Beispiel für eine Sprungstelle:
Ein Beispiel für eine Sprungstelle:
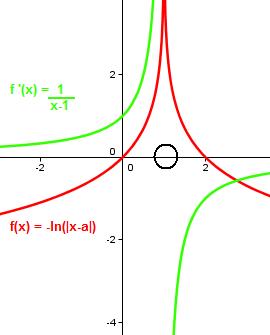
Lernstoff
|
|
4.3 Minima
|

 

|
Ganz analog dazu definiert man nun Minima:
Ein sogenanntes Minimum einer Funktion ist ein Punkt x = a, dessen Funktionswert f(a) zumindest
für einen kleinen Bereich um diesen Punkt (also links und rechts auf der x-Achse) der kleinste
Funktionswert ist.
Oder Mathematisch:
Beim Punkt x = a liegt ein Minimum f(a), wenn gilt:
f(a) &le f(x) in einer näheren Umgebung von a.
Betrachten wir auch hier ein Beispiel:
f(x) = (x-1)² +1
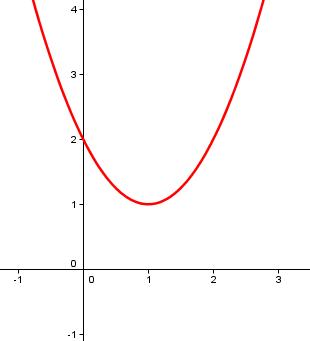 Im Bereich x < 1 ist sie streng monoton fallend, im Bereich x > 1 streng monoton steigend:
Im Bereich x < 1 ist sie streng monoton fallend, im Bereich x > 1 streng monoton steigend:
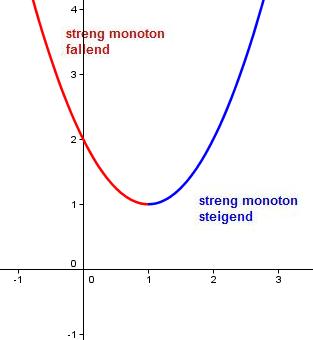 Für die Ableitung f’(x) = 2x -2 gilt:
f‘(x) < 0 für x < 1
f‘(x) > 0 für x > 1
Für die Ableitung f’(x) = 2x -2 gilt:
f‘(x) < 0 für x < 1
f‘(x) > 0 für x > 1
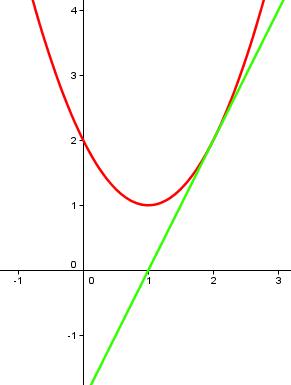 Alle Werte in der Umgebung von x = 1 sind also größer als f(1) = 1.
Damit hat f(x) bei x = 1 das Minimum f(1) = 1.
Ganz allgemein kann man sagen:
Wechselt die Ableitung f ‘(x) am Punkt x = a ihr Vorzeichen von - auf + , hat f(x) bei x = a
ein Minimum f(a)
Das kann nur bei einer 0-Stelle der Ableitung oder bei einer Sprungstelle der Ableitung passieren!
Alle Werte in der Umgebung von x = 1 sind also größer als f(1) = 1.
Damit hat f(x) bei x = 1 das Minimum f(1) = 1.
Ganz allgemein kann man sagen:
Wechselt die Ableitung f ‘(x) am Punkt x = a ihr Vorzeichen von - auf + , hat f(x) bei x = a
ein Minimum f(a)
Das kann nur bei einer 0-Stelle der Ableitung oder bei einer Sprungstelle der Ableitung passieren!
Lernstoff
|
|
4.4 Rätsel der Sphinx
|

 

|
 Vorsicht! Es stimmt zwar, dass ein Extremum bei einer 0-Stelle oder einer Sprungstelle der Ableitung
einer Funktion liegen kann, das muss aber nicht so sein! Worauf kommt es an, ob eine Funktion
bei einem Punkt auch wirklich ein Extremum hat?
Kannst du eine Funktion finden, deren Ableitung zwar an einem Punkt x = a eine 0-Stelle hat, wobei
aber die Funktion selbst kein Extremum bei x = a hat?
Skizziere den Graphen der Funktion und dessen Ableitung in dein Hausübungs-Heft und schreibe
dazu, was notwendig ist, damit eine Funktion wirklich ein Extremum an einem Punkt hat!
Eine mögliche Antwort findest du in folgendem Link. Versuche aber trotzdem selbst eine Antwort zu
finden!
Beispiel
Vorsicht! Es stimmt zwar, dass ein Extremum bei einer 0-Stelle oder einer Sprungstelle der Ableitung
einer Funktion liegen kann, das muss aber nicht so sein! Worauf kommt es an, ob eine Funktion
bei einem Punkt auch wirklich ein Extremum hat?
Kannst du eine Funktion finden, deren Ableitung zwar an einem Punkt x = a eine 0-Stelle hat, wobei
aber die Funktion selbst kein Extremum bei x = a hat?
Skizziere den Graphen der Funktion und dessen Ableitung in dein Hausübungs-Heft und schreibe
dazu, was notwendig ist, damit eine Funktion wirklich ein Extremum an einem Punkt hat!
Eine mögliche Antwort findest du in folgendem Link. Versuche aber trotzdem selbst eine Antwort zu
finden!
Beispiel
Übungsaufgabe
|
|
4.5 Randpunkte
|

 

|
Ist eine Funktion speziell nur auf einem eingeschränkten Teil definiert (Definitionsbereich), gibt es
noch eine letzte Möglichkeit, wo man Minima und Maxima auffinden kann. Nämlich an den
Randpunkten des Definitionsbeirechs.
Für ein solches Maximum oder Minimum muss die Ableitung der Funktion jedoch nicht
unbedingt das Vorzeichen wechseln!
Zwei Beispiele haben wir hier:
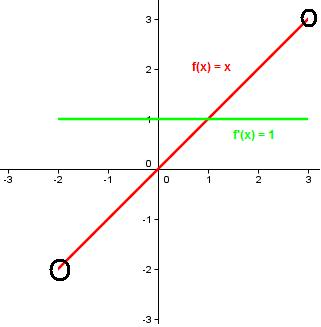
Die Funktion f(x) = x hat auf dem Definitionsbereich [-2,3] ein Minimum bei x = -2 und
ein Maximum bei x = 3, obwohl die Ableitung f‘ (x) = 1 nirgends das Vorzeichen wechselt!
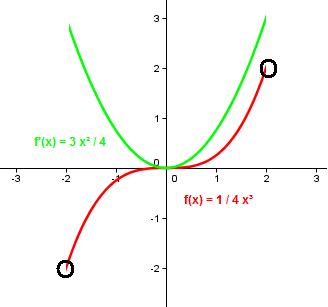
 Die Funktion g(x) = 1/4 x³ hat auf dem Definitionsbereich [-2,2] ein Minimum bei x = -2 und
ein Maximum bei x = 2, obwohl die Ableitung g‘ (x) = 3/4 x² nirgends das Vorzeichen wechselt!
Die Funktion g(x) = 1/4 x³ hat auf dem Definitionsbereich [-2,2] ein Minimum bei x = -2 und
ein Maximum bei x = 2, obwohl die Ableitung g‘ (x) = 3/4 x² nirgends das Vorzeichen wechselt!
Lernstoff
|
|
4.6 Rätsel der Sphinx
|

 

|
 Überlegt, wie ihr herausfinden könnt, ob der Randpunkt eines Definitionsbereichs ein Minimum oder
ein Maximum ist!
Diskutiert auch in Gruppen!
Hinweis: Unterscheidet zwischen den oberen und unteren Randpunkten der Definitionsbereiche!
Überlegt, wie ihr herausfinden könnt, ob der Randpunkt eines Definitionsbereichs ein Minimum oder
ein Maximum ist!
Diskutiert auch in Gruppen!
Hinweis: Unterscheidet zwischen den oberen und unteren Randpunkten der Definitionsbereiche!
Übungsaufgabe
|
|
4.7 Kritische Punkte
|

  
|
Die Stellen, an denen man bei einer Funktion ein Extremum finden kann, nennt man ‘kritische Punkte‘.
Als kritische Punkte kommen in Frage:
-0-Stellen der Ableitung der Funktion
-Stellen, an der die Ableitung der Funktion nicht definiert ist. (Hier könnte eine Sprungstelle sein!)
-Falls ein fixer Definitionsbereich vorgegeben ist : Randstellen des Definitionsbereichs
Schreibe diese Definition in dein Schulübungsheft!
Definition (Lernstoff)
|
|
4.8 Globale Extrema
|

  
|
Ein weiterer wichtiger Punkt zu Extrema ist die Unterscheidung zwischen lokalen und globalen
Extrema.
Eine Funktion kann ja mehr als ein Maximum oder Minimum haben.
Ein globales Maximum ist das Maximum einer Funktion, dessen Funktionswert größer
als alle anderen Funktionswerte der Funktion sind.
D.h. es ist das Maximum mit dem größten Funktionswert.
Ein globales Minimum ist das Minimum einer Funktion, dessen Funktionswert kleiner
als alle anderen Funktionswerte der Funktion sind.
D.h. es ist das Minimum mit dem kleinsten Funktionswert.
Sehen wir uns das anhand eines Beispiels an:
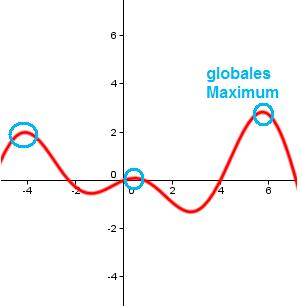
Die folgende Funktion hat an allen blau gekennzeichneten Stellen ein Maximum, aber nur ein
globales Maximum!
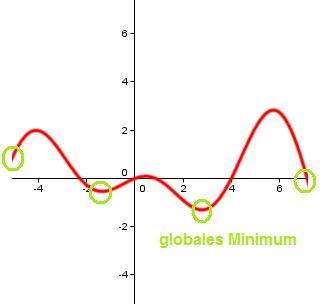
 Die Funktion hat an allen grün gekennzeichneten Stellen ein Minimum, aber nur ein
globales Minimum!
Die Funktion hat an allen grün gekennzeichneten Stellen ein Minimum, aber nur ein
globales Minimum!
 Es gibt keinen rechnerischen Trick um ein globales Maximum von anderen Maxima zu unterscheiden.
Man muss hier alle Maxima bestimmen und dann das mit dem größten Funktionswert suchen!
Dasselbe gilt für Minima:
Man muss alle Minima bestimmen und dann das mit dem kleinsten Funktionswert suchen!
Schreibe die Definition von globalen Minima und globalen Maxima in dein
Schulübungs-Heft!
Es gibt keinen rechnerischen Trick um ein globales Maximum von anderen Maxima zu unterscheiden.
Man muss hier alle Maxima bestimmen und dann das mit dem größten Funktionswert suchen!
Dasselbe gilt für Minima:
Man muss alle Minima bestimmen und dann das mit dem kleinsten Funktionswert suchen!
Schreibe die Definition von globalen Minima und globalen Maxima in dein
Schulübungs-Heft!
Definition (Lernstoff)
|
|
4.9 Rätsel der sphinx
|

 

|
 Nun denn, Reisender! Ich habe wieder ein paar Rätsel für dich. Versuche sie zu lösen und
lass dich nicht in die Irre führen!
Lass dir Zeit und lies die Fragestellungen genau durch!
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Nun denn, Reisender! Ich habe wieder ein paar Rätsel für dich. Versuche sie zu lösen und
lass dich nicht in die Irre führen!
Lass dir Zeit und lies die Fragestellungen genau durch!
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Übungsaufgaben
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



