|
3.1 Definition - Stammfunktion
|

  

|
Eine Funktion F(x) nennt man Stammfunktion einer reellen Funktion f(x), wenn an jeder Stelle im Definitionsbereich von f(x) gilt:

Eine Stammfunktion ist eine differenzierbare Funktion F(x), die dadurch gekennzeichnet ist, dass ihre Ableitung F‘(x) mit f(x) übereinstimmt.
Das Darstellen der Stammfunktion einer reellen Funktion f(x) kann als Umkehroperation zum Differenzieren dargestellt werden. Die Bezeichnung Stammfunktion wird verwendet, wenn man eine bestimmte Stammfunktion F(x) meint. Die Gesamtheit aller Stammfunktionen bezeichnet man jedoch als das unbestimmte Integral.
Die übliche Schreibweise wird dafür verwendet:

Die additive Konstante C, welche beim Ableiten wegfällt, ist von sehr großer Bedeutung, da es zu jeder Funktion beliebig viele, unterschiedliche Stammfunktionen gibt, die sich nur in der Konstante C unterscheiden!
Niemals die additive Konstante C vergessen!
Für ein besseres Verständnis, möchte ich Sie gleich mit einem Beispiel konfrontieren:
Sei F(x) = x4+x³ eine differenzierbare Funktion.
Fragestellung: Ist F(x) eine Stammfunktion der Funktion f(x)=4x³+3x²?
Überprüfung: F'(x) = 4x³+3x² = f(x) ⇒ F(x) ist Stammfunktion von f(x).
Berechnung des unbestimmten Integrals von f(x):
⇒ ∫f(x)dx = 4x³+3x²+C.
Zur Veranschaulichung dienen die folgenden zwei Abbildungen:
1. Abbildung: Funktion f(x)
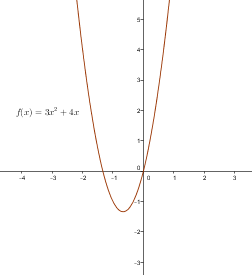
2. Abbildung: Eine bestimmte Stammfunktion F(x) von f(x)

Schreiben Sie die wichtigsten Informationen zum Thema "Stammfunktion" in ihr Lerntagebuch und wiederholen Sie ihre Eintragungen!
Lernstoff, Eintrag in das Lerntagebuch
|
|
3.4 Integraltabelle
|

 

|
Ihre Aufgabe: Wiederholen Sie die bisher gesammelten Erfahrungen zum Differenzieren und Integrieren und beweisen Sie die Tabelle der Grundintegrale durch die Umkehroperation der Integration!
Die beiliegende Tabelle sollen Sie selbstverständlich für die weiteren Kapitel des Lernpfades verwenden!
Wiederholung, Übungsaufgabe, Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



