|
5.1 Definition - Flächen zwischen Kurven
|

  

|
In diesem Kapitel werde ich ihnen genau darstellen, wie man den Flächeninhalt zwischen Kurven berechnet. Zuerst wollen wir den Flächeninhalt eines Gebietes bestimmen, das oben durch die Funktion f(x), unten durch die Funktion g(x) und links und rechts durch das Intervall [a,b] begrenzt ist. Da die Funktionen f(x) und g(x) beliebige Funktionen sind, müssen wir den Flächeninhalt in der Regel mithilfe eines Integrals bestimmen.
Sind f und g auf dem gesamten Intervall [a,b] stetig mit f(x) ≥ g(x), so ist der Flächeninhalt des Gebiets zwischen den Kurven f(x) und g(x) von a und b das Integral über (f – g) von a bis b:

Um diese Definition anzuwenden, ist es sehr sinnvoll den Graphen der Funktion zu visualisieren. Durch die Darstellung der Funktionen können Sie jetzt erkennen, welche Kurve die obere Kurve f und welche die untere Kurve g ist. Weiters können Sie anhand der Skizze die Integrationsgrenzen erkennen, sofern diese nicht vorab gegeben sind. Oftmals ist es jedoch der Fall, dass man für die Bestimmung der Integrationsgrenzen die Schnittpunkte der beiden Graphen bestimmen müssen. [dh. f(x) = g(x) muss nach x aufgelöst werden] Wenn die Integrationsgrenzen bestimmt sind, kann man die Funktion (f – g) integrieren, um den Flächeninhalt zwischen den Schnittpunkten zu berechnen.
Um ein besseres Verständnis gegenüber der Berechnung der Fläche zwischen Kurven zu erhalten, werde ich ihnen die Vorgehensweise anhand eines Beispiels genau darstellen.
Aufgabenstellung:
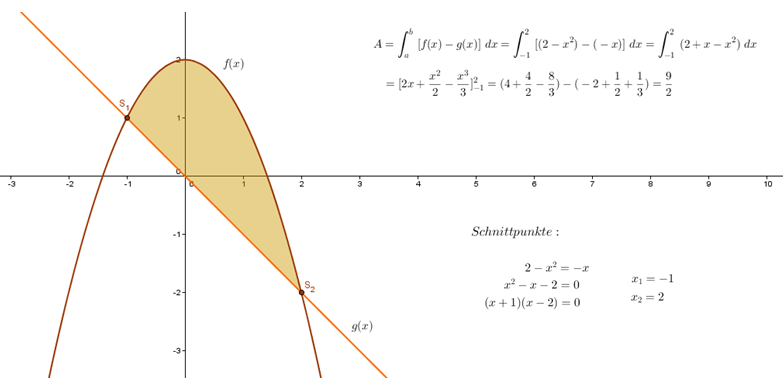
Bestimmen Sie den Flächeninhalt des von der Parabel f(x) = 2 – x² und der Geraden g(x) = –x eingeschlossenen Gebiets.
Zunächst visualisiere ich die beiden Funktionen. Um die Integrationsgrenzen zu bestimmen, muss ich die Schnittpunkte der Graphen bestimmen. Die Integrationsgrenzen ergeben sich also aus der Lösung des Gleichungssystems f(x) = 2 – x² = – x = g(x).
Das Gebiet reicht von x = -1 bis x = 2. Die Integrationsgrenzen sind a = -1, b = 2. Daraus ergibt sich folgende Lösung:
Eintrag in das Lerntagebuch, Lernstoff
|
|
5.2 Inhalte von Flächen zwischen zwei Funktionsgraphen
|

 
|
Lesen Sie sich im Buch Mathematik verstehen 8 die Seite 27 genau durch! Bearbeiten Sie im Anschluss folgende Beispiele:
2.16
2.18 c)
2.19 a) und b)
2.21 b)
2.32 1)-3)
|
|
5.3 Übungsbeispiele - Fläche zwischen Kurven
|

 

|
Im beiliegende Dokument finden Sie zahlreiche Übungsbeispiele, die sich mit dem Berechnen der Fläche zwischen zwei Graphen beschäftigen. Die einzelnen Arbeitsaufträge entnehmen Sie bitte direkt aus der Datei! Viel Spaß beim Durchführen der Übungen!
Übungsaufgaben, Selfchecking Test, Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



