|
4.1 Definition - Bestimmtes Integral
|

  

|
Im vorherigen Kapitel haben wir die Ermittlung von Stammfunktionen genauer kennengelernt und können daraus schließen, dass sich die Stammfunktionen einer Funktion f(x) durch die additive Konstante C unterscheiden. In diesem Kapitel definiere ich den Kern dieses Lernpfades, nämlich das bestimmte Integral. Im Rahmen dieses Lernpfades verwenden wir das bestimmte Integral hauptsächlich zur Flächenberechnung.
Zunächst betrachten wir die folgende Abbildung, in der das Intervall [a,b] in n Teilintervalle unterteilt wird. Für die Bildung der unterschiedlichen Teilintervalle wählen wir beliebige Punkte x1,x2,…,xn-1.

Eine derartige Zerlegung des Intervalls bezeichnet man auch als Partition des Intervalls [a,b].

Nach dieser Unterteilung wählt man in den einzelnen Teilintervallen wiederum beliebige Zwischenpunkte c1, c2 , …,cn. Dann bildet man die Summe:

Wenn man x0 = a, xn = b und xk - xk-1 = Δxk schreibt, kann man die Summe einfach als

schreiben. Diesen Ausdruck bezeichnet man als Riemannsche Summe von f(x) für die jeweilige Zerlegung. In der dargestellten Abbildung entspricht diesem Ausdruck die Summe der Flächen der einzelnen Rechtecke. Da wir bereits durchbesprochen haben, dass die endliche Summe nur eine Annäherung an die tatsächliche Fläche unter der Kurve ist, müssen wir die Anzahl der Unterteilungen (n) gegen unendlich laufen lassen, wobei gleichzeitig die Länge der einzelnen Teilintervalle gegen 0 geht.
Falls die Riemannsche Summe gegen einen Grenzwert konvergiert, welcher unabhängig von der Wahl der Zerlegung ist, dann bezeichnen wir genau diesen Grenzwert als das bestimmte Integral der Funktion f(x) zwischen dem Intervall [a,b].
Die übliche Schreibweise:

Die Funktion f(x) nach dem Integralzeichen wird Integrand genannt, a ist die untere Grenze, b die obere Grenze. Die Variable x ist die Integrationsvariable und „dx“ bezeichnet man als das Differential. Wie bei Variablennamen üblich, ist x dabei eine beliebige Bezeichnung. Die Integrationsvariable kann auch anders genannt werden:
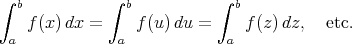
Die Schreibweise 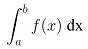 kann man folgendermaßen interpretieren: "Integral von f von x dx zwischen den Grenzen a und b". Das Integral ist erst dann berechnet, wenn Sie den Wert des Integrals bestimmt haben. kann man folgendermaßen interpretieren: "Integral von f von x dx zwischen den Grenzen a und b". Das Integral ist erst dann berechnet, wenn Sie den Wert des Integrals bestimmt haben.
Um die Berechnung von Flächen zu veranschaulichen, stelle ich ihnen ein einfaches Beispiel zur Verfügung:

Zunächst soll die Fläche unter dem Funktionsgraphen zwischen den Intervallgrenzen [a,b] bestimmt werden. Ist die Funktion f(x) eine auf dem Intervall [a,b] beschränkte reelle Funktion und F(x) eine Stammfunktion von f(x), so kann man das bestimmte Integral berechnen. Dem bestimmten Integral a∫b f(x) dx wird immer der Zahlenwert F(b) - F(a) zugeordnet!

Als Zwischenergebnis schreibt man grundsätzlich für F(b) - F(a) auch [F(x)]ba.
Kurze Zusammenfassung: Das bestimmte Integral ist bei Funktionen mit stets nichtnegativen Funktionswerten (siehe obiges Beispiel) eine Zahl, die den Flächeninhalt unter der Funktion f(x) zwischen den Grenzen a und b angibt. Die Zahl ist jene Fläche, die zwischen der x-Achse und dem Graphen von f(x) liegt. Links und rechts wird die Fläche von den Ordinaten in a und b begrenzt, wobei a die untere und b die obere Intervallgrenze darstellt. Bei stets negativen Funktionswerten ist der Wert des bestimmten Integrals negativ. Um den Inhalt der Fläche zu bestimmen, muss der Betrag des bestimmten Integrals verwendet werden.

Lernstoff, Eintrag in das Lerntagebuch
|
|
4.2 Anwendungen der Integralrechnung
|

  

|
Lesen Sie sich im Buch Mathematik verstehen 8 die Seiten 24 bis 25 genau durch! Bearbeiten Sie im Anschluss folgende Beispiele:
2.03 c)
2.04 d)
2.06 b)
2.07 a)
2.08 c)
2.09 c)
2.10 a) und b)
2.11 im Buch
2.12
2.13 b)
2.14 c)
Übungsaufgaben, Eintrag in das Lerntagebuch, Lernstoff
|
|
4.5 Übungsbeispiele - Bestimmtes Integral
|

 

|
Im beiliegende Dokument finden Sie zahlreiche Übungsbeispiele, die sich mit dem Berechnen des bestimmten Integrals beschäftigen. Viel Spaß beim Durchführen der Übungen!
Übungsaufgaben, Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



