|
7.1 Einleitung - Methoden
|

 
|
Nach den zahlreichen ausführlichen Kapitel, die einerseits die Grundlagen der Integralrechnung, als auch die wichtigsten Regeln behandelt haben, nimmt dieses Kapitel eine sehr zentrale Rolle ein. Es geht hierbei darum, wie man zu beliebigen Funktionen eine Stammfunktion ermitteln kann. Während die Ableitung nach bestimmten Grundkonzepten hergeleitet werden kann, kann das Integrieren nicht nach bestimmten „Rezepten“ vollzogen werden. Aus diesem Grunde gibt es für die Integralrechnung einige wichtige Techniken, die sehr hilfreich sein können, um schwierige Integrale ohne Probleme zu lösen.
|
|
7.2 Erklärung der Techniken
|

  

|
Partielle Integration:
Mit dieser Technik kann man Integrale vereinfachen, die in der Form

vorliegen. Die partielle Integration kann als Analogon zur Produktregel der Differentialrechnung aufgefasst werden.
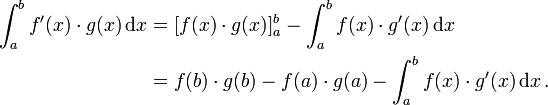
Die Gleichung der partiellen Integration kann man sich vielleicht leichter merken, wenn man Sie anhand von Differentialen schreibt. [u = f(x) und v = g(x)]
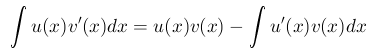
In dieser Gleichung wird das Integral ∫u v' in einen Term umgeformt, der jetzt das Integral ∫v u' enthält. Die Gleichung ist also nur dann nützlich, wenn das zweite Integral einfacher zu berechnen ist als das erste. Dazu müssen die Funktionen u und v geschickt gewählt werden.
Hinweis: Bei vielen Integralen gibt es für diese Wahl mehrere Möglichkeiten.
Bei der partiellen Integration versucht man also, ein Integral, das man so nicht lösen kann, in ein anderes umzuformen, dessen Lösung einfacher ist. Bewährt hat sich im Allgemeinen folgenden Strategie:
Man wählt als v' den Teil des Integrals inklusive dx, dessen Stammfunktion man kennt. Die Funktion u ist dann der restliche Teil des Integranden. Die Stammfunktion v von v' sollte möglichst einfach gewählt werden. Eine Integrationskonstante in v ist nicht notwendig; sie würde auf der rechten Seite von der Gleichung sowieso wegfallen.
Für ein besseres Verständnis werde ich Ihnen anhand eines Beispieles die Technik der partiellen Integration genauer darstellen.
Beispiele zur partiellen Integration
Lernstoff, Eintrag in das Lerntagebuch
|
|
7.4 Erklärung der Techniken
|

  

|
Integration durch Substitution:
Durch die Einführung einer neuen Integrationsvariablen wird ein Teil des Integranden ersetzt, um das Integral zu vereinfachen und so auf ein eventuell bekanntes oder einfacher handhabbares Integral zurückzugreifen. Grundlage für die Substitutionsregel ist die Umkehrung zur Kettenregel aus der Differentialrechnung.
In der Regel wendet man eine Substitution nur dann an, wenn der Integrand aus einer Verkettung von Funktionen besteht. Besteht der Integrand aus einem Produkt verketteter Funktionen f(g(x)) und der Ableitung g‘(x) der inneren Funktion g(x), dann kann die Methode der Substitution angewendet werden.
Die Methode der Substitution auf bestimmte Integrale wird erweitert, indem die Integrationsgrenzen direkt verändert werden müssen. Die folgende Formel zeigt, wie sich die Integrationsgrenzen ändern, wenn die Integrationsvariable durch Substitution geändert wird.

Zur Anwendung der Formel nehmen wir dieselbe u-Substitution u = g(x) und du = g'(x) dx vor wie bei der Berechnung des entsprechenden unbestimmten Integrals. Wir integrieren dann das transformierte Integral bezüglich u vom Wert g(a) (dem Wert von u an der Stelle x = a) bis zum Wert g(b) (dem Wert von u an der Stelle x = b).
Um ein besseres Verständnis für diese Methode zu erlangen, werden ich Ihnen anhand von Beispielen die Methode der Substitution genauer darstellen:
Beispiel zur Integration mit Substitution
Lernstoff, Eintrag in das Lerntagebuch
|
|
7.6 Übungsbeispiele - Integrationstechniken
|

  
|
Im beiliegende Dokument finden Sie zahlreiche Übungsbeispiele, die sich mit dem Berechnen des bestimmten Integrals anhand von unterschiedlichen Methoden beschäftigen. Die weiteren Arbeitsaufträge finden Sie direkt in der Datei! Viel Spaß beim Durchführen der Übungen!
Übungsaufgaben, Lernstoff, Selfchecking Test
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



