Bei der Definition des bestimmten Integrals als Grenzwert der Summen der einzelnen Teilintervalle einer Partition haben wir uns von links nach rechts durch das Intervall [a,b] bewegt. Was passiert jedoch, wenn wir es stattdessen von rechts nach links durchlaufen. Wenn wir also bei x0 = b starten und bei xn = a enden? Da wir der Rückwärtsintegration keine genaue Bedeutung zugewiesen haben, definieren wir:

Die nachfolgende Datei zeigt ihnen die grundlegenden Eigenschaften von Integralen in Form von Regeln, wobei Sie die beiden eben diskutierten Eigenschaften auch in der Datei finden. Diese Regeln werden ihnen mit Sicherheit bei der Berechnung von Integralen sehr nützlich sein.

Die Graphen innerhalb des Dokumentes sind Graphen positiver Funktionen. Die Regeln gelten aber für allgemeine integrierbare Funktionen.
Sind f und g über dem Intervall [a,b] integrierbar, so erfüllt das bestimmte Integral die folgenden Rechenregeln:
Rechenregeln für bestimmte Integrale
Falls etwaige Rechenregeln noch nicht ganz verständlich sind, hoffe ich, dass ich ihnen diese anhand eines Beispiels präzise erklären kann. Zur Illustration einiger Regeln nehme ich an, dass
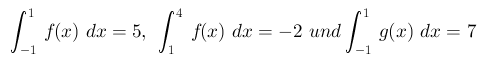
ist. Dann gilt:

Als letztes Beispiel werde ich noch auf eine weitere Rechenregel für bestimmte Integrale eingehen. Diese Regel bezieht sich nur auf symmetrische Funktionen. Aus diesem Grunde definieren wir:

Ich betrachte als Beispiel die Funktion f(x) = x4 - 4x2 + 6. Um die Symmetrie der Funktion zu beweisen, visualisiere ich ihnen diese Funktion.

Weil die Funktion die Gleichung f(-x) = f(x) erfüllt, erhalten wir eine gerade Funktion auf dem symmetrischen Intervall [-2,2]. Also gilt:

Eintrag in das Lerntagebuch, Lernstoff
|



