Die Idee dahinter ist, dass in der Natur von irgendetwas entweder nichts da ist, oder eines davon, oder zwei, drei oder noch mehr. Die natürlichen Zahlen entstehen daher sozusagen "natürlich" durch Zählen von Dingen bzw. durch wiederholte Addition von 1 zur vorhergehenden Zahl. Die grundlegenden Eigenschaften natürlichen Zahlen sind daher:

• Null ist die kleinste natürliche Zahl
• Zu jeder natürlichen Zahl n gibt es eine Nachfolgerin n+1 und zu jeder natürlichen Zahl außer 0 gibt es auch eine Vorgängerin.
• Zwischen einer natürlichen Zahl n und ihrer Nachfolgerin n+1 liegt keine weitere natürliche Zahl. Das heißt, dass die Elemente am Zahlenstrahl dargestellt, einzelne, isolierte Punkte sind.
• Es gibt keine größte natürliche Zahl. Es gibt also auch unendlich viele natürliche Zahlen.
• Die natürlichen Zahlen sind geordnet. D.h. für zwei unterschiedliche, beliebige natürliche Zahlen m und n kann man immer sagen, welche davon größer und welche kleiner ist.

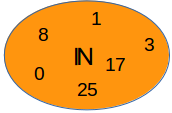
Damit ist die Menge der natürlichen Zahlen definiert als ℕ={0, 1, 2, 3, ...}. Aber Achtung: in manchen Büchern oder Aufgaben gehen AutorInnen davon aus, dass die natürlichen Zahlen erst bei Eins beginnen! Das wird manchmal damit begründet, da es in der Natur ja nicht "Nichts" gibt ... Bei uns hier beinhaltet die Menge ℕ aber immer auch die Zahl 0, außer es steht etwas anderes dabei. Wenn die Menge der natürlichen Zahhlen erst mit 1 beginnt, so wird diese Menge geschrieben als ℕ^* = {1, 2, 3, 4, ...}

Oft betrachtet man auch nur manche Teilmengen von ℕ, wie z.B.: ℕ_g:={0, 2, 4, 6, ...} die Menge aller geraden Zahlen, ℕ_u:={1, 3, 5, 7, ...} der Menge aller ungeraden Zahlen. Die Punkte deuten an, dass die Elemente in der Menge ewig nach dem gleichen Schema so weitergehen. Das bedeutet auch, dass die Mengen unendlich groß sind.

Die natürlichen Zahlen verwenden wir immer dann, wenn wir z.B. Dinge abzählen oder Reihenfolgen bestimmen.

Überlege dir einmal, welche Rechenoperationen alleine mit natürlichen Zahlen durchführbar sind. Kann man zwei beliebige natürliche Zahlen addieren und erhält als Ergebnis immer eine natürliche Zahl?

Das scheint zu funktionieren, oder? Egal welche natürlichen Zahlen du nimmst, das Ergebnis der Addition wird immer eine natürliche Zahl sein. Geht das auch mit der Multiplikation? Subtraktion? Division? Kannst du bei diesen 3 Grundrechnungsarten vielleicht jeweils zumindest ein Gegenbeispiel finden? Für welche schon, für welche nicht? Probiere es aus!

Wichtig: Liegt für beliebige Paare von natürlichen Zahlen das Ergebnis einer bestimmten Rechenoperation wieder in den natürlichen Zahlen, so sagt man die natürlichen Zahlen sind abgeschlossen bezüglich dieser Operation.

Bezüglich welcher Grundrechnungsarten sind die natürlichen Zahlen abgeschlossen?

Eine wichtige Berechnungsart ist, den Quotienten und Rest einer ganzzahligen Division zu bestimmen. Bei vielen Computeranwendungen wird z.B. sehr oft nur mit ganzen Zahlen gerechnet, weil das viel Schneller geht. Je nach Aufgabe wird dabei manchmal nur der Quotient weiterverwendet, manchmal ist nur der Rest interessant.

Jede Division von natürlichen Zahlen lässt sich als Quotient und Rest darstellen. Z.B. 17:5 = 3 mit 2 Rest, also 17 = 3*5 + 2.

Dies lässt sich auch mit der eng zusammenhängenden Subtraktion sehr gut erklären. Wie oft kann 5 von 17 subtrahiert werden ohne dass das Ergebnis negativ wird? Nennen wir diese Anzahl "q". Bleibt am Ende der q Subtraktionen noch ein Rest "r" übrig oder geht es sich genau aus? Bei obigem Beispiel: 17-5-5-5 = 2. Wir können also 3-mal die Zahl 5 von 17 subtrahieren. Am Ende bleibt ein Rest von 2.

Die Division von zwei Zahlen beliebigen a,b ∈ ℕ lässt sich in der Form a = q·b + r darstellen. Wir definieren:
a div b = q ... Quotient der ganzzahligen Division von a durch b
a mod b = r ... Rest der ganzzahligen Division von a durch b

Wenn man die Divison mit Rest verstanden hat, kann man auch die Teilbarkeit von natürlichen Zahlen ganz einfach definieren:

Eine Zahl a∈ℕ heißt teilbar durch eine Zahl b∈ℕ, wenn der Rest der ganzzahligen Division 0 ist. Geschrieben als: a∣b ("a teilt b") bzw. a∤b ("a teilt b nicht").

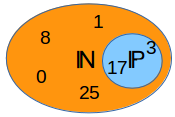
Sehr viele natürliche Zahlen lassen sich als Produkt von anderen natürlichen Zahlen darstellen, also z.B. 6 = 2 ·3. Das geht aber bei 7 nicht! Warum? Passiert das nur wenigen Zahlen? Welche Zahlen sind das?

Diese Teilmenge von ℕ nennt sich die Menge der Primzahlen ℙ. Wenn diese Zahlen also nicht als Produkt von zwei anderen Zahlen dargestellt werden können, gilt umgekehrt auch, dass sie durch keine andere natürliche Zahl teilbar sind, außer durch 1 und durch sich selbst. "Manche" natürliche Zahlen sind also Primzahlen und alle Primzahlen sind natürliche Zahlen. Also gilt: ℙ⊂ℕ

Eine Primzahl ist eine natürliche Zahl größer als 1, wenn sie nur durch 1 und sich selbst teilbar ist.

Recherchiere, wie viele Primzahlen es gibt! Suche einen mathematischen Beweis dafür wie viele es gibt und schreibe ihn dir in für dich verständlichen Sätzen ins Lernjournal!

Alle natürlichen Zahlen lassen sich auch als sogenannte Primfaktoren darstellen. Wiederhole noch einmal, auf welche Weise sich diese Primfaktorenzerlegung berechnen lässt und übe dies an ein paar Beispielen!