|
3.1 Was sind ganze Zahlen?
|

 

|
Natürliche Zahlen sind ganze Zahlen. Aber es gibt noch wesentlich mehr! Alle natürlichen Zahlen bleiben auch noch ganz wenn sie ein negatives Vorzeichen haben.
- Zu jeder ganzen Zahl n gibt es eine Nachfolgerin n+1 und zu jeder ganzen Zahl gibt es auch eine Vorgängerin n-1.
- Zwischen zwei direkt benachbarten ganzen Zahlen n und n+1 liegt keine weitere ganze Zahl. Das heißt, dass die Elemente am Zahlenstrahl dargestellt, einzelne, isolierte Punkte sind.
- Es gibt keine größte und keine kleinste ganze Zahl. Es gibt also auch unendlich viele ganze Zahlen.
- Die ganzen Zahlen sind geordnet. D.h. für zwei unterschiedliche, beliebige ganze Zahlen m und n kann man immer sagen, welche davon größer und welche kleiner ist, also ob gilt m<n oder m>n.
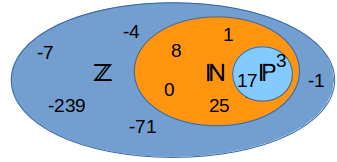
Die Menge der ganzen Zahlen ist also definiert als ℤ = { ..., -3, -2, -1, 0, 1, 2, 3, ...}.
Das Symbol "-" hat mehrere verschiedene Bedeutungen bzw. Auswirkungen:
- Es ist das Operationszeichen für die Subtraktion, wie z.B. bei 53 - 17 = 36
- Es kann das Vorzeichen einer ganzen Zahl sein, wie z.B. -32
- Oder das Symbol zur Berechnung der sogenannten Gegenzahl einer ganzen Zahl n∈ℤ: -(5) = -5 oder -(-3) = 3
Zeichne dir einmal eine beliebige Zahl n∈ℤ (egal ob positiv oder negativ) auf dem Zahlenstrahl ein. Welche Zahl liegt genau symmetrisch gegenüber dem Nullpunkt? Das ist die sogenannte Gegenzahl von n, mathematisch -(n) = -n.
Lernstoff
|
|
3.3 Teilbarkeit von ganzen Zahlen
|

  
|
Teilbarkeit ist natürlich auch bei ganzen Zahlen eine wichtige Eigenschaft, die z.B. im Bereich der Kryptographie (Verschlüsselung) eine wichtige Rolle spielt. Im folgenden Kapitel eines Lernpfades dazu findest du interessante Erweiterungen des Begriffs der Teilbarkeit auf ganze Zahlen.
Kapitel über die Teilbarkeit von ganzen Zahlen
Mithilfe der Teilbarkeitseigenschaft bezüglich einer konkreten Zahl, wird die Menge der ganzen Zahlen in sogenannte Restklassen eingeteilt. Dadurch wird es möglich, bei bestimmten Aufgaben viel einfacher zu rechnen. Ein Beispiel: Willst du wissen wie spät es in 75 Stunden ist, so ist es nicht notwendig, tatsächlich 75 Stunden in die Zukunft zu rechnen. Die Uhrzeiten des Tages wiederholen sich ja alle 24 Stunden. Also reicht es, sich zu überlegen, wie viele ganze Tage in 75 Stunden enthalten sind und nur den Rest nach der ganzzahligen Division von 75 durch 24 zur aktuellen Uhrzeit dazu zu rechnen. 75 mod 24 = 3. Wenn es also jetzt z.B. 11 Uhr ist, dann ist es in 75 Stunden 14 Uhr. Denn in 75 Stunden ist es gleich spät wie in 3 Stunden, wie in 27 Stunden oder wie in 51 Stunden. Die Zahlen 3, 27, 51, 75, ... sind bezüglich 24 in der gleichen "Restklasse". Im folgenden Kapitel eines Lernpfades findest du eine mathematischere Formulierung:
Kapitel zu Restklassen
Lernstoff, Vertiefung
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



