Mit den ganzen Zahlen kann man im täglichen Leben schon sehr viel machen. Aber viele Fragen lassen sich mit ganzen Zahlen nicht beantworten.

Innerhalb der ganzen Zahlen ist es nun schon möglich, problemlos beliebige Zahlen zu addieren, subtrahieren und zu multiplizieren. Nur das Dividieren funktioniert immer noch nicht für alle, sondern nur für manche Elemente n∈ℤ. Wir bauen nun ausgehend von ℤ eine neue Menge, die auch bezüglich der Division (bis auf 0) abgeschlossen ist.

Die Menge der rationalen Zahlen ist definiert als ℚ = { z/n | z∈ℤ ∧ n∈ℕ\{0}}. Das bedeutet, die Menge ℚ besteht aus allen Brüchen, die im Zähler eine ganze und im Nenner eine natürliche Zahl außer der Null haben. Überlege dir, warum es nicht notwendig ist, auch den Nenner durch Elemente aus ℤ zu definieren!

• Jede rationale Zahl lässt sich wieder als Punkt auf der Zahlengeraden darstellen.
• Zwischen jedem beliebigen Paar von rationalen Zahlen liegt eine weitere rationale Zahl.
• Es gibt keine größte und keine kleinste rationale Zahl. Es gibt also auch unendlich viele rationale Zahlen.
• Die rationalen Zahlen sind natürlich auch geordnet. D.h. für zwei unterschiedliche, beliebige rationale Zahlen m und n kann man immer sagen, welche davon größer und welche kleiner ist, also ob gilt m<n oder m>n.

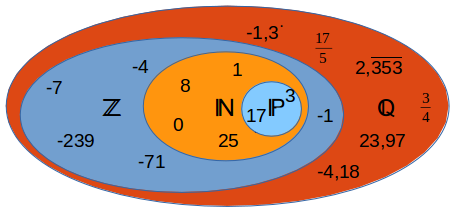
Jede ganze Zahl ist natürlich auch eine rationale Zahl, denn jedes n∈ℤ lässt sich auch als Bruch der Form n/1 darstellen, was wiederum Element von ℚ ist. Somit ist ℤ eine Teilmenge von ℚ oder ℤ⊂ℚ

Rationale Zahlen haben im Gegensatz zu den natürlichen oder ganzen Zahlen keine Nachbarn. Man kann nämlich selbst wenn man einen vermeintlichen Nachbarn zu einer rationalen Zahl nennt, zwischen den beiden eine (genauer nachgedacht sogar unendlich viele) weitere Zahlen finden!

Überlege dir: wenn ich dir zwei rationale Zahlen sage, kannst du mir eine Zahl nennen, die sicher dazwischen liegt? Versuche das einmal für 2/3 und 7/5! Wie kann man das für zwei beliebige Zahlen a,b∈ℚ verallgemeinern?

Oft scheint eine Zahl auf den ersten Blick keine rationale Zahl zu sein, wie z.B. -0,9285714285714... Oder lässt sich die Zahl vielleicht doch als Bruch darstellen?

Dividiert man Brüche aus um die Dezimaldarstellung zu erhalten, so erhält man manchmal als Ergebnis eine Dezimalzahl, die nach einigen Stellen abbricht. Wie z.B. bei 23/5 = 23:5 = 4,6 oder 19/20 = 19:20 = 0,95.

Andere Brüche als Dezimalzahl dargestellt hören jedoch nie auf und entwickeln eine periodische Darstellung, wie z.B. 1/3 = 1:3 = 0.3333333.... Aber auch -13/14 = -13:14 = -0.9285714285714... Auch diese Zahlen sind rationale Zahlen:

• Dezimalzahlen mit einer endlicher Anzahl von Nachkommastellen.
• Dezimalzahlen mit unendlich vielen, aber periodischen Nachkommastellen. Die Kommastellen können sich nach einer, aber auch erst nach vielen Stellen wiederholen.

Finde heraus, wovon es abhängt, ob Brüche beim Ausdividieren endlich oder unendlich viele, aber periodische Dezimalstellen entwickeln! Recherchiere wovon dies abhängt und rechne dir selbst einige Beispiel durch. Wie kann man diese rationale Zahlen mit endlichen oder unendlich periodischen Dezimaldarstellungen in Brüchen darstellen? Schreibe dir die Erklärungen und Vorgehensweisen in dein Lernjournal!

Bestimmte Mengen werden auch als "dicht" bezeichnet. Recherchiere was dieser Begriff bedeutet! Kannst du auch einen für dich verständlichen mathematischen Beweis dafür finden ob ℚ dicht ist?