| Dir ist bestimmt schon aufgefallen, dass die Negativen Zahlen am Zahlenstrahl aussehen wie ein Spiegelbild der Positiven Zahlen. Aber welche Negative Zahl ist denn nun größer, und welche kleiner? Lies dir folgende Diskussion über dieses Thema durch und überlege, wem du mehr zustimmst. Findest du, dass Peter Recht hat oder glaubst du, dass Susanne richtig liegt?
Peter: Wenn ich 5 Euro Schulden habe, dann hab ich mehr Schulden als wenn ich nur 3 Euro ausgeborgt habe. Also muss -5 größer als -3 sein.
Susanne: Aber wir haben doch vorher gelernt, dass Schulden nicht in Minuszahlen angegeben werden! Schau, wenn ich -5 Euro am Konto habe, habe ich einen niedrigeren Kontostand, als wenn ich nur -2 Euro am Konto habe. Deshalb muss -5 kleiner als -2 sein.
Peter: Okay, in dem Fall hast du vielleicht recht. Aber was, wenn es -10°C hat? Dann ist das ja eine größere Kälte als bei -2°C. Dann hab ich wieder Recht.
Susanne: Aber auch hier muss es doch so sein, dass -10°C eine niedriger Temperatur ist als -2°C, oder? Also müsste doch -10 wieder kleiner sein als -2.
Aber wer von den beiden hat denn nun Recht? Wirf einen Blick auf das folgende Bild und überlege dir, welche Seite die Darstellung von Peters Meinung ist und welche Seite die Darstellung von Susannes Meinung ist.
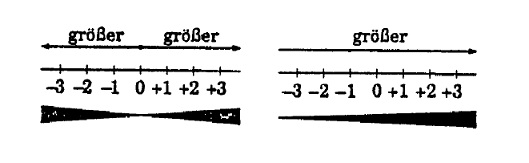
Peter und Susanne sind sich noch immer nicht einig, wer denn nun schlussendlich Recht hat. Da greift Marianne in die Diskussion ein. Sie sagt: "Ihr werdet doch bestimmt nicht bestreiten, dass 4 kleiner als 5 ist, oder?" Marianne schreibt die Ungleichung auf die Tafel.
4 < 5
Dann sagt sie: "Wenn wir nun auf beiden Seiten 3 abziehen, stimmt die Ungleichung noch immer."
Also schreibt sie auf die Tafel:
1 < 2
"Wenn wir jetzt noch mal 3 abziehen, kommt folgendes raus."
-2 < -1
"Also ist -2 ganz sicher kleiner als -1."
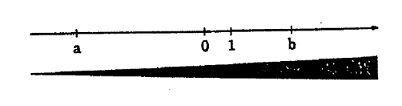
Marianne hat Recht. Die Ordnung der Negativen Zahlen ist genau gleich, wie bei den Positiven (und NICHT GESPIEGELT!), also eine Zahl (a), die am Zahlenstrahl weiter links liegt als eine andere Zahl (b), ist kleiner (also a < b)
Aufgabe: Lade folgende Datei herunter und drucke das Dokument aus. Erledige die Aufgaben und klebe das Übungsblatt in dein Schulübungsheft.
Ungleichungen.pdf
So, nun hast du schon ein ganzes Stück geschafft. Du kennst jetzt den erweiterten Zahlenstrahl sowie das erweiterte Koordinatensystem, du kannst Punkte darin einzeichnen und Negative Zahlen nach ihrer Größe ordnen. Einen großen Teil hast du schon geschafft! :-)
|



